LLMWhisperer Text Extractor-v1

LLMWhisperer is technology that presents data from complex documents to LLMs in a way they’re able to best understand it.

Getting started with LLMWhisperer Text Extractor

info

When you sign up for LLM whisperer, you will be automatically subscribed to Tier-1: Free 100 Pages Per Day plan.By using this plan you can, Process up to 100 pages a day completely free! No credit card required.To increase the usage limit,visit LLM whisperer plans

1. Sign-up a LLM Whisperer account and sign in.

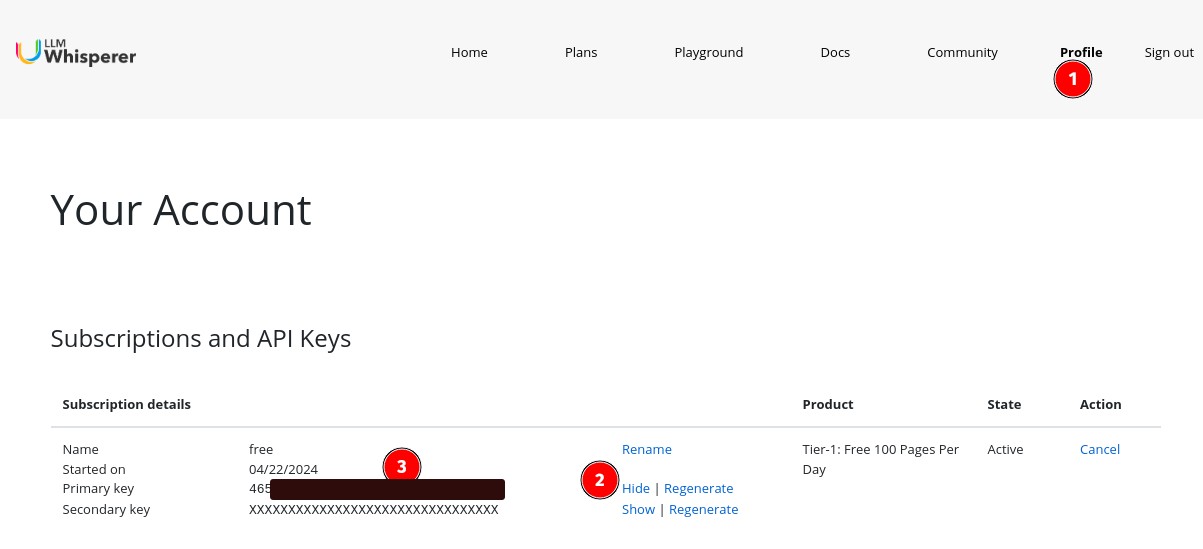
2. To get the API key click on "Profile" from the top navigation menu and then click on "show" to reveal the API key.

   

Setting up the LLM Whisperer connector in Unstract

Now that we have an API key from LLM Whisperer, we can use it to set up a Text Extractor profile on the Unstract platform. For this:

• Sign in to the Unstract Platform

• From the side navigation menu, choose Settings 🞂 Text Extractor

• Click on the New Text Extractor button.

• From the list of Text Extractor, choose LLMWhisperer. You should see a dialog box where you enter details.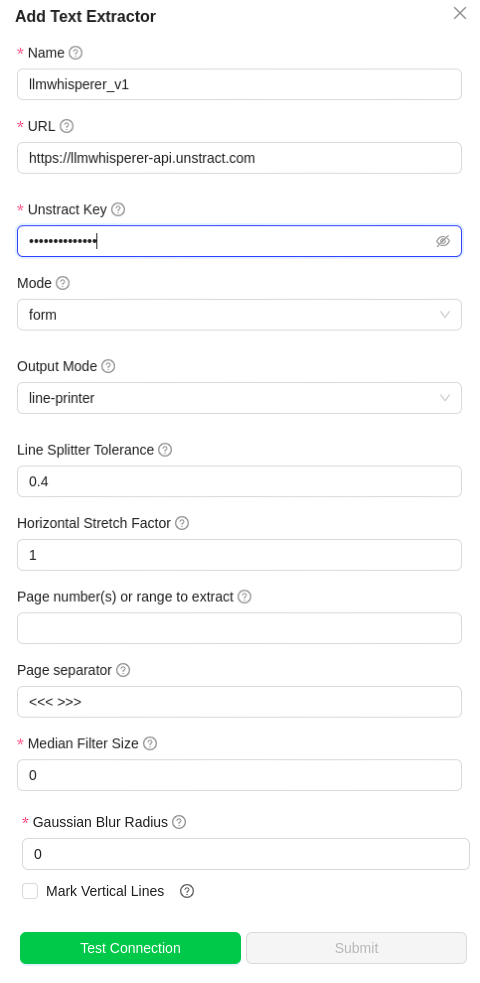

  

• For Name, enter a name for this connector.

• Leave the URL field to the default value.

• In Unstract Key, enter the key created in the above section.

• In Mode, choose

  • Native Text - To process text based files.
  • Low Cost - To process high quality pdf documents.
  • High Quality - To process Medium/low quality scanned PDFs and Handwritten documents.
  • Form - To process pdf with Checkbox and radio button detection
  • Check the below image for the comparison of modes

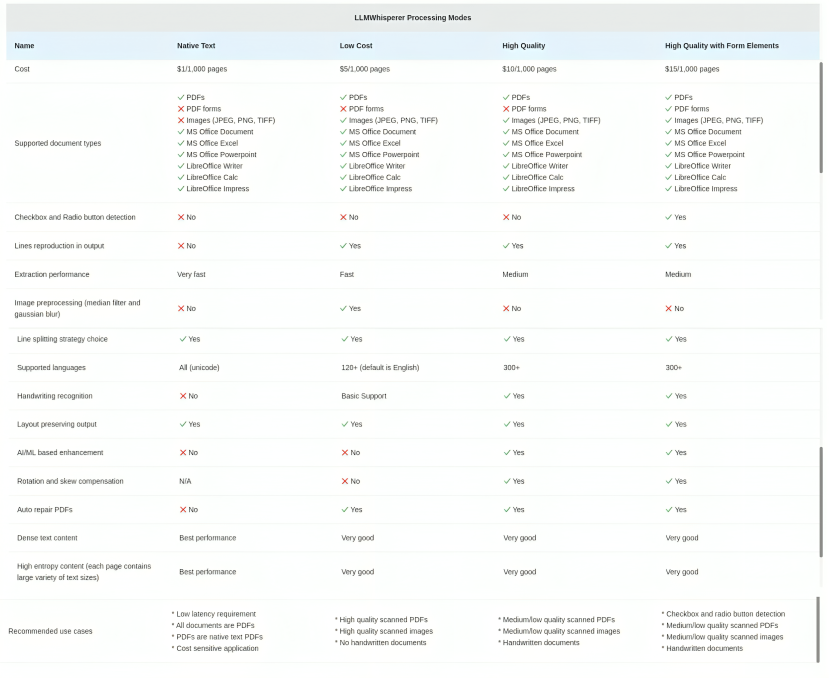
• In Output Mode, choose

  • layout_preserving - To extract the text line by line.
  • text - Keeps the context of the document in place.

• Line Splitter Tolerance - Default value is 0.4 .Reduce this value to split lines less often, increase to split lines more often. Useful when PDFs have multi-column layout with text in each column that is not aligned.

• Horizontal Stretch Factor - Default value is 1 .Increase this value to stretch text horizontally, decrease to compress text horizontally. Useful when multi-column text merge with each other.

• Page number(s) or range to extract- Specify the range of pages to extract (e.g., 1-5, 7, 10-12, 50-). Leave it empty to extract all pages.

• Page separator - Specify a pattern to separate the pages in the document (e.g., <<< {{page_no}} >>>, <<< >>>). This pattern will be inserted at the end of every page. Omit page_no if you don't want to include the page number in the separator.

• Mark Vertical Lines & Mark Horizonatal Lines

  • Both buttons must be in the same state (either both checked or both unchecked) for the operation to proceed.
  • If checked, it will extract the tables structure(border and internal lines) with dotted lines.Check this buttons if the table is outlined properly in the document.

• For Median Filter Size enter the window size. For eg, if input is 3, then filter window will be considered as 3*3.

  • A median filter reduces noise by replacing each data point with the median of its neighbors, effectively smoothing the data while preserving edges. The window size determines the extent of smoothing: a larger window size increases noise reduction but can blur edges, whereas a smaller window size maintains detail but is less effective at noise removal.

• For Gausian Blur Radius enter the blur radius.

  • Gaussian blur is a filter that smooths images by averaging pixel values with their neighbors, where the weights decrease with distance according to a Gaussian distribution. The radius, or standard deviation of the Gaussian function, controls the extent of blurring: a larger radius results in more blurring and a smoother image, while a smaller radius preserves more of the original details but provides less noise reduction.

• Leave other values to its default.

• Click on Test Connection and ensure it succeeds. You can finally click on Submit and that should create a new Text Extractor Profile for use in your Unstract projects.